My Erdős Number below 6 degrees of separation
Paul Erdős was a Hungarian mathematician who authored or co-authored hundreds of publications across a wide variety of disciplines. He was so prolific that a certain level of prestige is associated to having co-authored a paper with him. The idea for the Erdős Number came from another mathemetician, Casper Goffman. This has now turned into a kind of science cult, in the same way that the Bacon number (actually a newer concept stemming from the Erdős Number) has in acting (see here). Those who have co-authored with Erdős are given an Erdős number of 1. Someone who has never written a paper with Erdős, but who has co-authored a paper with one of his co-authors are given an Erdős number of 2, and so on with increasing degrees of separation. As noted by Lenski, while the ranks of those with 6 degrees of separation from Erdős and Bacon are quite high, very few people have an Erdős-Bacon Number.
For a long time, I've been pestering my mathatically inclined collaborators to find out what their Erdős number is so that I can plot my own. It turns out that I need not have bothered as my line is more direct than I had thought.
My first attempt equalled six degrees of separation:
Daniel Kleitman published many papers with Erdős, and has an Erdős number of 1
Lior Pachter has an Erdős number of 2, having co-authored a publication with Daniel Kleitman.
Richard Lenski has an Erdős number of 3, having co-authored a publication with Lior Pachter.
Jonathan Losos has an Erdős number of 4, having co-authored a publication with Richard Lenski.
Anthony Herrel has an Erdős number of 5, having co-authored a publication with Jonathan Losos.
I therefore have an Erdős number of 6, having co-authored a publication with Anthony Herrel
Thus my collaborators have either an Erdős number of 7 or lower (if they've got a more direct line to Erdős). It could be that my Erdős number is lower, or will get lower. Stay tuned for any updates!
Here are the relevant publications:
Beerenwinkel, N., Pachter, L., Sturmfels, B., Elena, S.F. and Lenski, R.E., 2007. Analysis of epistatic interactions and fitness landscapes using a new geometric approach. BMC Evolutionary Biology, 7(1), 1-12.
Blount, Z.D., Lenski, R.E. and Losos, J.B., 2018. Contingency and determinism in evolution: Replaying life’s tape. Science, 362 (6415).
Erdös, P. and Kleitman, D.J., 1968. On coloring graphs to maximize the proportion of multicolored k-edges. Journal of Combinatorial Theory, 5(2), pp.164-169.
Kleitman, D. and Pachter, L., 1998. Finding convex sets among points in the plane. Discrete & Computational Geometry, 19(3), pp.405-410.
Measey, G.J., & Herrel, A. 2006. Rotational feeding in caecilians: putting a spin on the evolution of cranial design. Biology Letters 2, 485-487.
But then my friend [and collaborator] Ben Stevenson [Erdős number 5] pointed out that the American Mathematical Society has their own Erdős calculator:
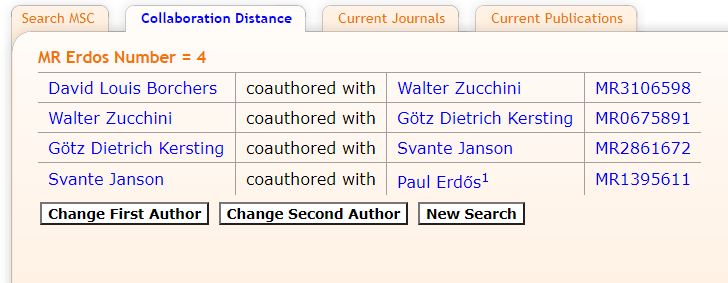
David [who was the first person I asked many years back] it turns out has an Erdős number of 4. As David and I published a few times, my Erdős number is actually 5.
Here are the relevant publications
Antille, A., Kersting, G., Zucchini, W. (1982) Testing symmetry. J. Amer. Statist. Assoc. 77, 639–646.
Borchers, D. L., Zucchini, W., Heide-Jørgensen, M. P., Cañadas, A., Langrock, R. 2013 Using hidden Markov models to deal with availability bias on line transect surveys. Biometrics 69 (3), 703–713.
Erdős, P., Janson, S., Łuczak, T., Spencer, J. (1996) A note on triangle-free graphs. Random discrete structures (Minneapolis, MN, 1993), 117–119, IMA Vol. Math. Appl., 76, Springer, New York,
Janson, S., Kersting, G. 2011 On the total external length of the Kingman coalescent. Electron. J. Probab. 80, 2203–2218.
Measey, G.J., Stevenson, B., Scott, T, Altwegg, R and Borchers, D. (2017) Counting chirps: acoustic monitoring of cryptic frogs. Journal of Applied Ecology 54: 894–902 https://doi.org/10.1111/1365-2664.12810 pdf